Air conditioning basic principles
The basis for air conditioning practice lies in thermodynamics principles and processes of heating and cooling air on the laws of heat exchange from elementary physics, and both the design and operation of refrigerating and heating equipment.
It is creating the desired “condition” of the air in an enclosed space, with controlled temperature and moisture content (humidity), depends on knowledge from a branch of physics called psychometry. Distribution of conditioned air to occupied areas, the introduction of outside air (called ventilation), and the removal of “stale” air are all problems of another mechanical energy is usually involved in these flow processes.
Maintaining the indoor temperature at desired levels, against outdoor extremes of heat and cold, involves the principles of heat transfer.
Every aspect of the air conditioning problem is concerned with one or more principles of fundamental physics. We will review several physical principles such as temperature, heat density, specific gravity, pressure, energy, work, and power.
Temperature
Temperature is a measure of the degree of “hotness” or “coldness” of a body or substance. Touch and feel tell us that fire is hot and that the winter wind is cold. For centuries the human senses were the only meaningful measure of temperature. Still, the senses differ from one person to another and vary from one season of the year to another, and consequently, they are quite unreliable. The accurate measurement of temperature is expressed in degrees, as determined by thermometers. Hand-held thermometers used in air conditioning work are usually alcohol- or mercury-filled. Changes in temperature of the surrounding air cause expansion and contraction of the liquid in the bulb, resulting in a rise or fall of the liquid level in the tube. The temperature is read off the scale at the top of the liquid column.
Thermometers take many forms. Remote-reading dial thermometers often have the sensing bulb and connecting tube filled with a gas. Changing temperatures cause the gas pressure to vary, and this results in the pointer moving across the dial. Thermocouples generate weak electric currents as a result of temperature differences, and these currents actuate a meter that can be calibrated to read temperatures accurately.
Thermometers take many forms. Remote-reading dial thermometers often have the sensing bulb and connecting tube filled with a gas. Changing temperatures cause the gas pressure to vary, and this results in the pointer moving across the dial. Thermocouples generate weak electric currents as a result of temperature differences, and these currents actuate a meter that can be calibrated to read temperatures accurately.
The Celsius temperature scale
The Celsius temperature scale is used throughout most of the world, (formerly Centigrade) scale. There are 100 equal degrees between its fixed points, which are the boiling point and freezing point of pure water at atmospheric pressure. The Celsius scale has the advantage of being decimalised and is therefore very convenient to use in many fields of scientific research.
The Fahrenheit temperature scale
About 1715, the German scientist Fahrenheit devised the temperature scale, which bears his name and which is the scale still widely used in the United States. The Fahrenheit scale of temperature is based on two fixed points which use pure water at atmospheric pressure as the standard. The boiling point of water at atmospheric pressure is marked as 212 degrees Fahrenheit (°F) and the freezing point of water is marked as 32°F. There are 180 equal degrees between the boiling point (bp) and the freezing point (fp) of water. The scale is extended above the boiling point and below the freezing point to measure higher and lower temperatures.
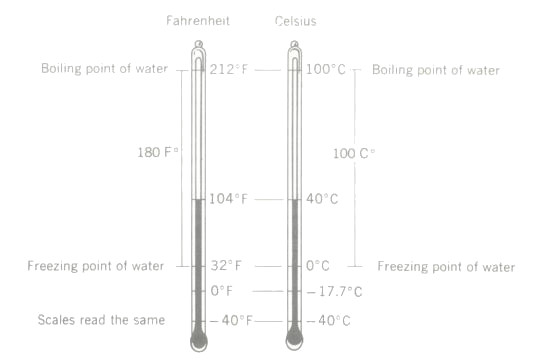
Fahrenheit and Celsius temperature scales compared. Note that the two scales have the same reading at -40°

Those were the days, a temperature logger! How many have seen this in action before?
The nature of heat
The philosophers of ancient times believed that heat was an invisible fluid, flowing from a hot object to a colder one. The term caloric (from the Latin word for “heat”) was applied to this fluid. It was not until Robert Boyle (1627-1691) and Sir Isaac Newton (1642-1727) that the concept of heat as internal molecular energy began to take form.
The classic experiments of Benjamin Thompson (Count Rumford) (1753-l814) are most often cited as the first conclusive evidence offered in support of the theory that heat is the energy of motion of molecules, atoms, and subatomic particles.
Thompson, about 1795, was supervisor of a Bavarian ordnance plant, and the boring of brass cannon was one of several machining operations carried out under his direction. He became interested in observing and measuring the tremendous amounts of heat produced in these drilling operations. Water was used to cool the drills, and the vital fact noted by Thompson was that as long as mechanical work was being done on the drills, heat was produced. It would point to an inexhaustible supply of “caloric” within the brass, a conclusion the absurdity of which Thompson pointed out in various papers presented to the scientific societies of Europe. In these papers, the theory that heat is a form of energy was first developed. Subsequent workers, among them Joule, Faraday, and Maxwell, produced experimental data that supported Thompson’s theory. The old concept of heat as a mysterious fluid was abandoned, and the new idea of heat as the energy of molecular motion was adopted. This idea or concept is often referred to as the kinetic-molecular hypothesis (kinetic, from the Greek, meaning “in motion”).
Molecules and heat
According to the molecular theory of matter, all substances (elements and compounds, solids, liquids, and gases) composed of millions of tiny submicroscopic particles called molecules. The term molecule describes the smallest possible particle of a given substance which still retains all the properties of the material. According to the theory, molecules are so related to one another in size and distance apart that in gases the average distance apart is always many times the diameter of a single molecule. Molecules are, in turn, made up of smaller particles called atoms; and atoms themselves are composed of the so-called elemental particles, which include, but are not limited to protons, electrons, and neutrons.
At ordinary temperatures, molecules are believed to be in constant motion but not all at the same speed, so that their individual energies differ. Many collisions between molecules must result, of course, and these cause a continual changing of the velocity of any given molecule. Molecular collisions are subject to the usual energy transformations governing collisions of finite, elastic bodies so that any loss of speed (energy) by one of two colliding molecules is accompanied by a gain of kinetic (energy) by the other.
The total amount of energy possessed by a given substance can be regarded as the sum of the energies of all its molecules, including their internal energies, resulting from such causes as rotation or vibration of atoms and electrons, and the potential energy of “binding forces” within atoms. Since the energy of any one molecule depends largely on its velocity, the total energy possessed by a body or substance (which may be made up of untold billions of molecules) depends on its total mass (that is, on the total number of molecules) and the average molecular velocity.
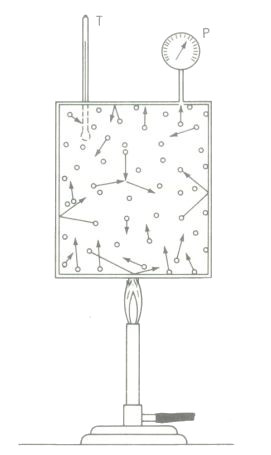
The diagram above illustrating the kinetic-molecular theory in gases. Heat energy increases molecular motion. Increased molecular velocities show up as increased temperature on thermometer T. Higher molecular velocities result in more frequent and more violent impacts on the walls of the container, which condition registers as an increased pressure on gauge P. Spaces between molecules are many times the molecular diameters. Collisions are frequent. Motion, not rest, is the normal condition. Total energy equals the sum of all the separate molecular energies, including their internal energies.
The molecular theory of matter leads us, then, to three important generalizations, all of them basic to a real understanding of air conditioning processes.
These are:
- Heat is a form of energy and the total heat energy possessed by a body or a substance is merely the sum of the energies of all its molecules.
- The temperature of a body or substance is an indication of heat intensity or degree of heat, and it is measured by thermometers.
- The molecules of a body or substance can be assumed to have a somewhat random distribution of velocities. Some molecules may be stationary at a given instant, others moving at a velocity associated with temperatures far below the freezing point of water, others at velocities associated with the boiling point of water, and still others at velocities so great as to be associated with the temperature of superheated steam.
To illustrate this random-distribution idea further, consider a beaker of water in which a thermometer reads 18°C. This means that the average of all the molecular velocities is such that the degree or intensity of heat is that associated with 18°C. In the beaker of water there may be some molecules with velocities associated with temperatures at or near absolute zero, some with velocities so high as to be associated with superheated steam, and a distribution of molecular velocities between these two extremes which results in an average degree of heat, or
temperature of 18°C.
The distribution of molecular velocities, though it approaches a random distribution, is not precisely that. James Clerk Maxwell (1831-1879) was able to show, from years of careful experimentation and theoretical considerations as well, that statistically, the molecules in a sample of gas do have a definite, though not entirely random, distribution of speeds.
Figure below shows the general form of the curve of probability distribution of molecular speeds. It is called a Maxwellian distribution curve.
Assuming such a probability distribution of molecular speeds to represent the situation in the beaker of 18°C water discussed above, it is interesting to think about what might happen if most of the higher-energy molecules (say all those represented by velocities plotted to the right of the dotted line FF in fugure above) could be drawn old in some way. What do you think would occur? Its implications for refrigeration and air conditioning are significant.
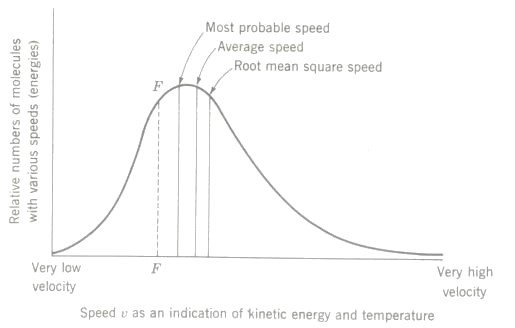
Maxwellian distribution of molecular velocities depicting the average molecular speed at any given instant is the characteristic that is indicated by a thermometer reading. Note that the curve is not symmetrical with respect to a vertical axis, and therefore a random distribution (in the statistical sense) is not indicated.
Measurement Systems
Two systems of measurement are in use in practice.
All the nations of the world; including Canada and the other British Commonwealth, have adopted the metric system. The U.S. Customary System (USCS), sometimes called the engineering system is primarily used in the United States.
Units of measurement
It is necessary at this point to review the units of measurement needed in the air conditioning industry. The fundamental units of measurement for all scientific and engineering work are length, mass, and time. The other well-known units that we often use are called derived units.

Units of measurement
Area
The standard units of area in metric for air conditioning purposes are the square meter (m2), the square centimeter (cm2), and the square millimeter (mm2). The square foot (sq ft or ft2), and the square inch (sq in. or in2) in US. Area is obtained by multiplying a length times a length, so area has the units of L X L, or L2.
Volume
Volume has the units L X L X L or L3. Metric units of volume are the cubic meter (m3) and the cubic centimeter (m3). The liter (1000 cm3 ) is also frequently used as a volume unit in air conditioning. The standard unit of volume in US is the cubic foot (cu ft or ft3).
Velocity or Speed
Velocity has the dimensions of length divided by time or L/T. The metric units of velocity frequently used in air conditioning are the meter per second (m/sec), and a lesser extent the centimeter per second (cm/sec). The minute is not usually used in metric calculations in air conditioning. Units of velocity in US are the foot per second (fps or ft/sec), and the foot Per minute (fpm or ft/min). The foot per minute (fpm) is the commonly used US unit for flow of air in ducts.
Force
Force has the same units as weight! in the English system. Weight is defined as the force of gravity acting on mass. The basic unit of force in the metric system is the newton (N), named for Sir Isaac Newton, the renowned English physicist of the seventeenth century. The earth’s gravity attracts a 1kg mass with a force of 9.81N at sea level at the equator. The factor 9.81 is the metric value of g, the acceleration of gravity at the earth’s surface, thus, g = 9.81 m/sec2. Even in some “metric countries” there is still a dual system of forces and weights. The newton is the official unit of force and of weight, but the older units, kilogram-force (kg-f, or kilo) and gram of force (gm-f) still find use in some everyday transactions. The newton is defined as that single unbalanced force that will give a mass of one kilogram an acceleration of one meter per second per second. The dimensions of the newton (N) are therefore kg.m/sec2.
Forces and weights in the US are measured in pounds, ounces, and grains.
Pressure
Pressure is defined as force per unit area. The basic unit of pressure in the SI system is the Pascal (Pa), but the kilopascal (kPa) is a more useful measure for the range of pressures encountered in air conditioning practice. The pascal is a pressure of one newton per square meter ( 1 Pa = 1 N/m2). Pressures in metric countries are also measured in centimeters of mercury (cm.Hg) and millimeters of mercury (mm.Hg). One atmosphere (atm) = 76 cm.Hg = 760 mm.Hg.
The most common pressure unit in the US is the pound per square inch (lb/in2 or psi). Pressures are also measured in inches of mercury (in.Hg) and in inches of water (in.WG). One atmosphere pressure (1 atm) = 29.92 in.Hg or 407 in.WG.
Density
Density is defined as mass per unit volume. In the metric system the common units of density are the kilogram per cubic meter (kg/m3), the gram per cubic centimeter (g/cm3), and the gram per liter (g/liter or g/L). The symbol for density in the metric system is the Greek letter rho (ρ = m/V). Weight density is defined as weight per unit volume. It is designated by the letter D, and its units are pounds per cubic foot (lb/ft3). In air conditioning practice in the United States, it is weight density (D) that is almost always used.
Units of Work, Energy, and Power
Work is done when a force is exerted on an object, moving it through a measurable distance. Work done is equal to the product of force applied times the distance moved, and consequently the unit of work in the SI system is the newton-meter (Nm). This unit has the name joule (J) named for James Prescott Joule, a nineteenth century British physicist.
W= Fs
Work = force X distance
The unit of work in US units is the foot pound (ft.lb).
Energy is the Capacity to do Work
Energy represents a condition of motion, position, or molecular arrangement which could be expected to accomplish work under a given set of conditions. The joule (J) is the unit of energy in the metric system. The unit of energy in the USCS is also the foot-pound.
Power is defined as the rate at which work is done or as the work done per unit time.
P = W/t = Fs/t
The metric unit of power is the joule per second (J/sec), named the watt (W), in honor of James Watt, the Scotsman who perfected the reciprocating steam engine in the late 1700s.
Electric power is also expressed in watts (W) or kilowatts (kW). The conversion from metric or electrical units of power to USCS or mechanical units for this purpose is
1 hp = 746 W = 0.746 kW
1 kW = 1.34 hp
In the metric system the joule and the watt are common to both mechanical and electric power.
Density, Specific Gravity, and Specific Volume
Density is the measure of the “heaviness” of a substance.
Density is an important concept in the selection of materials for air conditioning systems. Since most substances expand and contract appreciably on change of temperature, the temperature is usually specified in tables of density. This is particularly true of gases, whose change of volume with temperature is considerable. The density of gases is also affected markedly by pressure changes and therefore tables of density for gases are always stated in terms of standard conditions of temperature and pressure (32°F, 29.92 in. Hg, or 0°C, 760 mmHg).
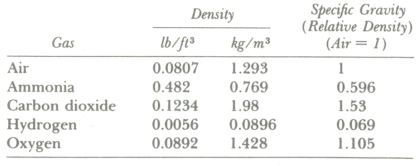
Specfic gravity is the ratio of the weight of a substance to the weight of an equal volume of water at 39°F. Pure water has its greatest density at 4°C (1000 kg/m3 or 1 g/cm3) or 39°F (62.4 lb/ft3).
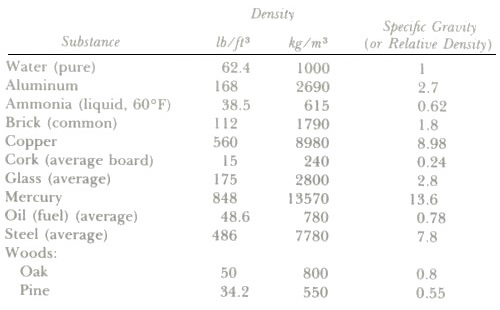
Density and specific gravity of some common substances
It should be noted that, since specific gravity is a ratio of densities, it is a dimensionless number. Since the density of water does not vary a great deal with temperature changes in the air conditioning range, corrections for water temperatures other than 4°C (39°F) are not ordinarily computed.
Specific Gravity of Gases
The specific gravity of gases is not referred to water as a standard but to air. In other words, the specific gravity of a gas tells how many times as heavy as air the gas is. Gas volumes are affected markedly by pressure and temperature variations, however, and all gas volumes must be corrected to standard conditions of temperature and pressure for density and specific gravity determinations.
Specific Volume of Gases
The specific volume (SpV) of a gas is an important concept in air conditioning. Specific volume is the reciprocal of density. In the metric system, specific volume is expressed in cubic meters per kilogram (m3/kg). Dry air at 0°C and 1 atm pressure (101.3 kPa) has a specific volume (metric units) 0.773m3/kg. In the US density is measured in pounds per cubic foot, and specific volume in cubic feet per pound.
Pressure and Its Measurement
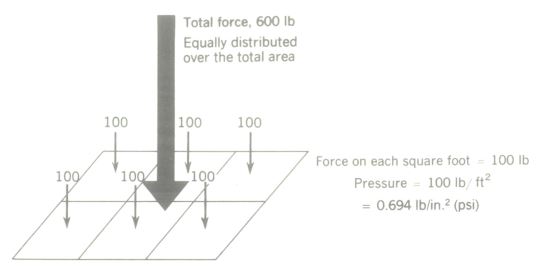
Pressure is force per unit area.
If a total force of 600 lb is evenly distributed over the 6 ft2 of area, the force on 1 ft2 would be 100 lb. The force acting on unit area is called pressure. Forces are ordinarily expressed in pounds, and area may be in either square feet (ft2) or square inches (in2) The corresponding pressure units are the pound per square foot (lb/ft2) and the pound per square inch (lb/in2) or as frequently abbreviated, psi.
In the metric system, forces are expressed in newtons (N) and areas in square meters. The unit of pressure is the N/m2, called the Pascal (Pa). The pascal is a very small unit of pressure, and the kilopascal (kPa) is a more practical unit.
1 kPa = 1000 Pa.
Pressure in Liquids
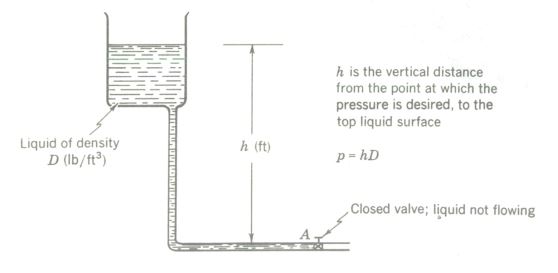
Pressure in nonflowing liquids (hydrostatic pressure) is caused by the actual weight of the liquid above the point being considered, in which case the pressure can be calculated from the basic formula of hydrostatics
p = hD
Pressure = depth X density
which gives pressure in pounds per square foot when h, the depth, is in feet and D, the density, is in pounds
Pressure in Gases
The pressure of gases in containers is caused, not by the weight of the gas, but by the continuous collision of gas molecules with the sides of the container. There is no simple relation for calculating gas pressures, and consequently gauges are always used for determining them.
Atmospheric Pressure
The earth’s atmosphere extends above the earth’s surface to a height of about 200 mi. The atmosphere is most dense at sea level and becomes more rarefied as altitude increases. Atmospheric pressure on a normal day at sea level is 14.7 psi. Atmospheric pressure is most commonly measured by an instrument called a barometer. The pressure of the atmosphere is due to the actual weight of air pressing down on unit area of the earth’s surface.
The standard mercury barometer consists essentially of a glass tube, previously evacuated, inverted in a small bowl of mercury. Normal atmospheric pressure is sufficient to support a column of mercury 29.92 in. or 760 mm in height.
Other liquids could be used in barometers, but since they are all less dense than mercury the length of the tube would have to be so long as to be cumbersome. For example, a water-filled barometer would have a liquid column about 33.9 ft high. Since the specific gravity of mercury is 13.6. As a suitable approximation, 34 ft of water is taken as the equivalent of 1 atm.
A form of barometer which uses no liquid but depends on a sensitive bellows which actuates a mechanical linkage to operate a pointer on a scale is called an aneroid barometer. Aneroids are more rugged in construction and more practical for industrial use than mercury barometers, although they Absolute pressure = gauge pressure are not so consistently accurate as the mercury type.
Normal atmospheric pressure can be expressed, in five different ways:
14.7 lb/in2
29.92 in. Hg
760 mmHg
33.9 ft water
101325 Pa
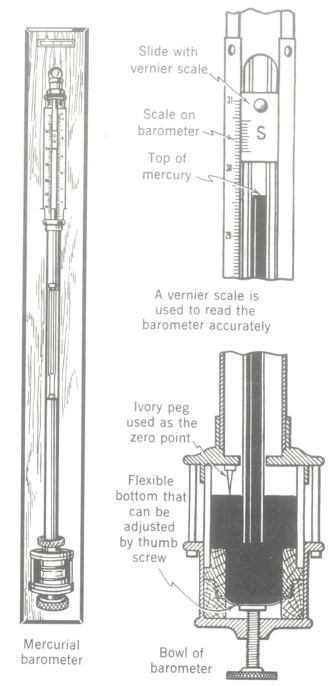
Barometers for the determination of atmospheric pressure. On the left a sketch of mercury barometer for vertical mounting on a wall. On the right details of mercury well and scale reading for mercury barometer.
Pressure Gauges
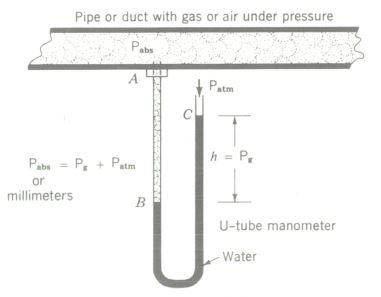
The principle of pressure measurement by using liquids in tubes, as exemplified by the mercury barometer, is utilized in pressure gauges of the U-tube or manometer type. Gas pressure in pipe A presses down on the water (or other liquid) in the left side of the U tube, depressing it to point B and elevating it to point C in the right-hand column.
The difference in elevation, or deflection h, is a measure of the gas pressure in the pipe. This pressure can be read directly from a scale expressed in inches or millimeters of mercury (if the U tube is mercury-filled) or in inches of water (if the tube is filled with water).
This latter unit, inches of water, is used in air conditioning work to measure the pressure of fuel gas in pipes and to measure the pressure of air in the ducts of air-distribution systems since these pressures are usually quite low.
Gauge Pressure and Absolute Pressure
The pressure obtained from readings on gauges is designated as gauge pressure. Analysis of the diagram above shows that the total pressure in the pipe A is the indicated gauge pressure plus the atmospheric pressure acting downward on the right-hand liquid column. This total pressure is called absolute pressure, and the following relation defines it:
Absolute pressure = gauge pressure + atmospheric pressure
Pabs = Pg + Patm
Absolute pressures are expressed in pounds per square inch, absolute (abbreviated psia), in pascals (Pa), and sometimes in inches or millimeters of mercury. Absolute pressures must always be used when dealing with the thermodynamic properties of refrigerants and with gases in general. Gauge pressures may be expressed as pounds per square inch, gauge (psig) or as inches of water, gauge (in. wg). Ordinarily, in industrial practice, the word “gauge” is not added, and readings are understood as being gauge pressures unless absolute specifically indicated.
Bourdon Gauges
U-tube, or manometer, gauges can be conveniently used only for low-pressure measurements. In air conditioning work the Bourdon-type gauge is most often used in order to measure the high pressures frequently encountered. Bourdon gauges will be found installed on compressors, refrigerant lines, water lines, steam lines, refrigerant cylinders, boilers, and similar equipment. Bourdon gauges are fitted with a dial and pointer. They can be calibrated to read in pounds per square inch, or in kilopascals, or in inches or millimeters of mercury directly.
Referring to the cutaway, the circular tube (T) is made of thin, flexible brass, one end (A) being free to move while the other end (B) is fixed. As the gauge is connected to the line, gas (or liquid) enters the tube and the resulting pressure flexes the thin brass causing the free (A) end to move outward. A linkage (L) is connected to a gear (G) which rotates the pointer (P), which moves across a scale calibrated to read directly in the desired pressure.
Pressure Gauges and Vacuum Gauges
Some Bourdon-type gauges are arranged to measure pressures both above and below atmospheric. These are called compound gauges. The positive readings are termed pressure readings, and the negative one being vacuum readings. Some vacuum gauges read pounds per square inch, absolute (psia), but the more common calibration is in inches of mercury. On the vacuum side the scale reads to 30 in., and the nearer the reading is to 30 inch, the lower is the absolute pressure. A 30-in. reading (actually 29.92), if attained, would indicate a perfect vacuum.
Vacuum gauges are used in testing refrigeration compressors and in measuring pressures in refrigerant lines and air distribution lines.

A Bourdon type pressure vacuum (compound) gauge, usually used at pump suction and compressors.