Properties of Air - Psychrometry

Psychrometry - Properties of Air

Air is the medium with which buildings are cooled and heated and their occupants made comfortable in summer and winter. Before a building can be air-conditioned, the air itself must first be “conditioned.” It should be reemphasized also at this point that conditioning air is not simply a matter of heating it or cooling it to some desired temperature. The complete process of air conditioning not only involves heating and cooling, but is also concerned with humidification and dehumidification, with ventilation that is, supplying the proper amount of “fresh” outdoor air, and with air cleaning (filtration) and air distribution. The final “condition point” of the air is not some agreed upon and fixed standard either, since human comfort itself is very difficult to define. Standards of human comfort vary with location on the earth, with climate, with the seasons of the year, with the life-style and habits of dress of the population, and with the nature of physical activity at the time.

Of all the properties that affect air conditioning processes, moisture content, or humidity, is perhaps the most important. Water vapor is almost always present in atmospheric air, and its presence, in small or large amounts, affects human comfort markedly. The study of air-water vapor mixtures is called Psychrometry.

The Composition of Air

Atmospheric air may be considered to be composed of

dry air,
moisture in the form of water vapor or steam, and
impurities such as smoke, dust, or noxious gases.

Each of these constituents poses part of the problem of air conditioning.

Pure, dry air is itself a mixture of several gases. The most important of these are oxygen and nitrogen. Varying amounts of carbon dioxide are also present; and SO are several inert gases such as argon, neon, helium, and krypton. By weight the percentage composition of dry air is approximately as shown below.

Nitrogen about 77%
Oxygen about 22%
Carbon dioxide about 0.04%
Other gases about 0.96%

In spite of the fact that air is a mixture, the constituents’ percentages remain relatively constant, and dry air may be considered, for our purposes, as a single gas of molecular weight 28.97. Under conditions of low pressure and temperature, dry air closely approximates an ideal or perfect gas and may be represented by the ideal gas laws with reasonable accuracy.

Today, pure air is a rare commodity, and the problems of air purification and filtration are becoming increasingly important and difficult. Dust, smoke, bacteria, pollen, traffic fumes, and other noxious gases are some of the contaminants most frequently found in air. Smoke, fumes, and noxious gases are more frequently found in cities or industrial areas, while dust and pollen are more typical of rural areas. Airconditioning systems ordinarily remove only those pollutants that are represented by particles in the air stream. Noxious gases, especially those gases that are water-soluble, can be removed by the installation of special equipment, but most residential air conditioning systems do not incorporate this feature. Some of these gases may dissolve in and be carried away with the condensate from the cooling coil, in summer operation.

In air conditioning, all these factors about the composition of air are a matter of concern. The control of temperature is unquestionably a primary purpose of any air conditioning system. Dust, pollen, smoke, and odors should be eliminated or reduced to a point conducive to human comfort and tolerance. Control of water vapor or humidity in air is of great importance since its presence has considerable effect upon human comfort and on many industrial processes. Air which is too dry affects the nasal passages and skin adversely and is damaging to some materials and furnishings. Air which is too moist makes people uncomfortable in both summer and winter. In space-age manufacturing, many products require precise control of temperature, humidity, and air purity in carefully controlled, clean room atmospheres.

Water Vapor in the Air

Air contains water vapor in widely varying amounts. In desert regions air is very dry, and in tropical jungles it is so moist that one can almost feel the wetness in the atmosphere. Proper control of the moisture content of air is of major importance to human comfort as well as to industrial processes, and humidity is one of the most difficult factors to control in an air conditioning system. Water vapor in the air is, in actuality, low-pressure-low-temperature steam, and it mixes with dry air on a strictly mechanical basis. At the temperature-pressure conditions encountered in most air conditioning calculations, water vapor may also be assumed to behave as an “ideal” gas. Although this assumption is not rigorously true, carefully performed experiments provide results which agree very closely (within 1 percent for normal temperatures) with results obtained from ideal gas relations. Such accuracy is normally sufficient for air conditioning calculations.

The Laws of Gases

Boyle ‘s law of gases states that with temperature constant, the volume of a gas is inversely proportional to its absolute pressure. As an equation Boyle’s law becomes

P1V1 = P2V2

Boyle’s law of gases can be verified experimentally by taking simultaneous pressure and volume readings as a quantity of gas is slowly compressed in a cylinder
fitted with a pressure gauge. The compression must take place with no temperature change (i.e., isothermally). A plot of the P-V readings shows that the area under the curve at any P-V condition equals that at any other P-V condition, or in other words, P1V1 = P2V2.

Charles’ law of gases states that with pressure constant the volume of a gas is directly proportional to its absolute temperature. As an equation, Charles’ law is

V1/V2 = T1/T2

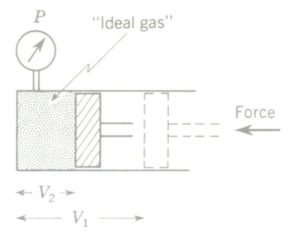
Gas in a cylinder is compressed in such a way that simultaneous pressure and volume readings can be recorded while the temperature remains constant. This process is termed isothermal compression.

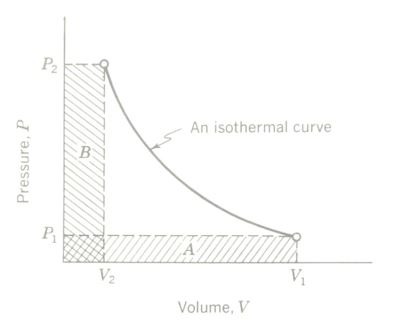
A graphical interpretation of Boyle’s law of gases. A plot of the P-V readings obtained. The isothermal curve is the locus of all P-V state points of the gas. Area A = area B, or P, V, = P2 V2 = k (a constant).

Charles’ law can be verified experimentally also. A cylinder fitted with a freely sliding piston in the image above is full of gas at atmospheric pressure. The cylinder is heated, and the temperature of the gas rises. This increased internal energy causes the gas to expand. Since the piston slides freely, the volume of the gas increases but pressure stays constant at 1 atm.

If simultaneous temperature and volume readings are plotted, a straight line results, as shown by the graph above. A and B represent two different P-T condition points of the gas, at 32°F (492°R) and at some higher temperature t°F (T°R), respectively. Careful measurements on the slope of the curve indicate that any gas expands by 1/492 of its volume at + 32°F for each Fahrenheit degree rise in temperature. Extrapolating the curve downward to the left until it intersects the horizontal axis gives a reading of-460°F at (theoretically) zero volume.

The value -460°F is therefore called absolute zero. Theoretically, at this temperature molecular motion ceases and the volume of any gas would be zero! It is this assumption which is inherent in the concept of an ideal gas. In reality such a gas does not exist, since all known gases liquefy long before reaching such low temperatures.

The Rankine Temperature Scale

An absolute scale of temperature has been devised using -460°F as its starting point. It is called the Rankine scale, and all problems involving gas volumes must be solved by using absolute temperatures.

Rankine temperature = Fahrenheit temperature + 460°F

The Kelvin Temperature Scale

There is also an absolute scale of temperature based on the Celsius temperature scale. It is called the Kelvin scale, and its absolute zero is -273°C. Intervals on the Kelvin scale are called Kelvins.

Kelvin temperature = Celsius temperature + 273°C

Absolute zero = zero K = 0°R = -460°F = -273°C

Note that 1 Kelvin = 1°C , and that the symbol K (for Kelvins) is written without the degree sign (°).

The General Gas Law-Ideal Gas

Combining Boyle’s and Charles’ laws of gases gives the general gas law,

P1V1/T1 = P2V2/T2

Another form of the general gas law is P V = mRT

where

P = absolute pressure on the gas, lb/ft²V = volume of given quantity of gas, ft³
m = mass (weight) of gas,” lb
T = absolute temperature, degrees Rankine (°R)
R = universal gas constant, 1545.3 divided by molecular weight of the gas

The units of R are (ft.lb)/(lb.mass)(°R).

Another useful form of the general gas equation may be obtained as follows:

If m is assumed to be 1 lb of gas, 1 becomes the volume per pound, or specfic volume (SpV) in cubic feet per pound, and

PSpV = RT for 1 lb of gas

This is a third form of the general gas law.

If V is assumed to be 1 ft³ of gas, m, on the other hand, becomes the mass (weight) per unit volume, or specific weight D, in pounds per cubic foot, also called density.

Note the relationship D = l/spv. Specific weight
(density) is the reciprocal of specific volume.

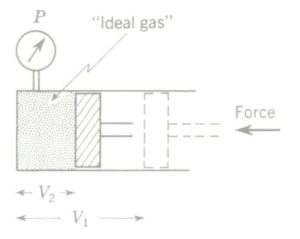
Experimental verification of Charles’ law of gases. Gas in a cylinder is heated and allowed to expand at constant Pressure as its temperature rises. Simultaneous temperature and volume readings are recorded.

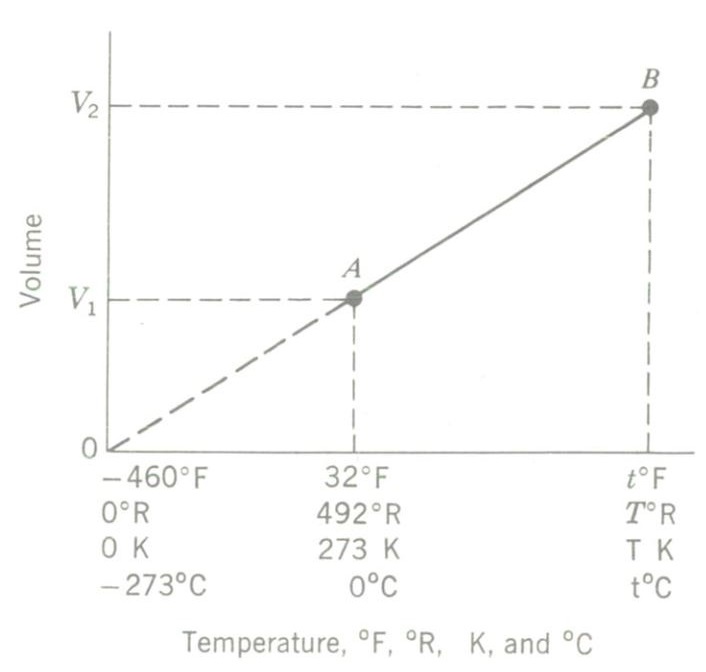
A plot of the V-T readings obtained results in a straight line, indicating that the two variables plotted are directly proportional to each other; that is V1/V2 = T1/T2

Values of the Gas Constant

The gas constant R may be obtained for any (ideal) gas by dividing 1545.3 by the molecular weight of the gas. Consequently,

Ra (the gas constant for air) = 1545.3/ 28.97 = 53.4 ft.lb/(lb)(°R)

Re (the gas constant for water vapor) = 1545.3/18 = 85.8 ft.lb/(lb)(°R)

Properties of Air-Water Vapor Mixtures

Both dry air and low-pressure water vapour behave as nearly ideal gases throughout the range of temperatures encountered in air conditioning practice, and they closely obey the ideal gas relations.

Dalton's Law of Partial Pressures

In l802, John Dalton (1766-1844) postulated the basic law concerning mixtures of perfect (ideal) gases: Cases occupying a common volume each fill that volume and behave as if the other gases were not present. Several very important relations may be stated as corollaries of this law.

The total mass of a mixture of air and water vapor is equal to the sum of the individual gas masses, mt = ma + mw.
Each gas occupies the same total volume, Vt = Va = Vw
The absolute temperature of the individual gases is the same as the temperature of the mixture, T = Ta = Tw.
The pressure of the gas mixture is equal to the sum of the pressures each gas would exert if it alone occupied the mixture volume (Dalton’s law of partial pressures), P = Pa + Pa.
The total heat (enthalpy) of the mixture is equal to the sum of the heat contents of the constituents, H = Ha + Hw.

The subscripts ‘a’ and ‘w’ in the above refer to dry air and water vapor, respectively. Dalton’s law, together with the general gas law, forms the basis for the derivation of the psychometric properties of air. In other words;

Barometric Pressure Pa comprises the partial pressure of dry air and the partial pressure of water vapor in the air, Pa = Pa + Pw. This is the pressure indicated by a barometer.
Atmospheric moisture is low-pressure-low-temperature steam.
The mixture temperature and the component gas temperatures are the same and this temperature is the dry-bulb temperature (db), or the temperature indicated by an ordinary thermometer.
Specific humidity W is defined as the weight (pounds) of water vapor per pound of dry air in a mixture at a stated dry-bulb temperature. Specific humidity is a measure of the actual moisture content in the air. Using the subscript ‘a’ where air is intended and the subscript ‘w’ where water vapor is intended.

the following equations may now be written for air-water vapor mixtures.

P = Pa + Pw – Dalton’s law of partial pressure

pava = maRaTa – General gas law

pwvw = mwRwTw – General gas law water vapour

where

P=total absolute pressure of air-water vapor mixture, lb./ft²Pa = partial pressure of dry air, lb/ft²
Pa = partial pressure of water vapor, lb/ft²
va = volume of dry air, ft³
vw = volume of water vapor, ft³ma = weight of dry air, lb
mw : weight of water vapor, lb

Ra = gas constant for air = 1545.3/28.97 = 53.4 ft-lb/(lb)(°R)

Rw = gas constant for water vapour = 1545.3/18 = 85.8 ft-lb/(lb)(°R)

The Moisture Content of Air-Humidity

Almost all air contains some moisture, and when it contains all the vapor it can hold, it is said to be saturated. The actual amount of water vapor that air can hold is governed by the mixture temperature. At low temperatures very little moisture is required to saturate air, and at high temperatures a great deal of vapor is required before saturation is reached. However, air is not often saturated and generally exists at a state well below saturation.

Water evaporates into the air over oceans or lakes and the air-water vapor mixture may be carried thousands of miles by winds as nonsaturated air. A sudden lowering of the temperature will reduce the ability of the air to “hold” the water vapor, and a saturated condition will be reached. Further lowering of the temperature will result in condensation of the water vapor, and some form of precipitation will result. Whether the precipitation will be fog, rain, snow, sleet, or hail depends on a variety of condition of air which are the proper concern of the meteorologist rather than the air conditioning engineer.

The general term for moisture content in air is humidity, which may be expressed in two ways as specific humidity and as relative humidity.

Specific humidity W is defined as the actual weight of water vapor mixed in a pound of dry air. It can be expressed as pounds of water vapor per pound of dry air or as grains of water vapor per pound of dry air.

Relative humidity is a measure of the degree of saturation of the air at any dry-bulb (db) temperature. It is an expression of percentage of saturation, with 100 percent relative humidity indicating saturated air and 0 percent relative humidity indicating perfectly dry air. Relative humidity RH is rigorously defined as the ratio of the actual partial pressure of the water vapor to the saturation partial pressure at the dry-bulb temperature.

RH = pw/psat x 100

where psat = saturation partial pressure of water vapor at dry-bulb temperature.

The ratio of specific humidities, actual versus saturated, is termed percentage saturation, and it too is frequently used to calculate values of relative humidity. In practice, both of these methods are used to calculate RH, but the ratio of partial pressures provides greatest accuracy and information.

RH = Wactual/Wsat x 100

Dew Point

If a mixture of dry air and water vapor is cooled, the ability of the air to hold water will be reduced, and a saturated condition will be reached. Further lowering of the temperature will result in condensation of the water vapor or the formation of dew. The dew-point temperature of the mixture is defined as the temperature at which water vapor starts to condense as the mixture is cooled. It is important to note that an air-water vapor mixture must be cooled to the dew point to remove or condense water vapor. The partial pressure of the water vapor in a mixture is the vapor pressure measured at the dew-point temperature. It is noted that, for a given barometric pressure, the partial pressure of the water vapor determines the moisture content of the air. Since dew-point temperature determines this vapor pressure, the dew-point temperature is a specific indicator of the moisture content of air.

It is worth noting that, despite the drop in dry bulb temperature, the some condition might be less comfortable for some people owing to the increase in relative humidity. It is also significant that the relative humidity can increase without change in specific humidity or actual moisture content. At saturation the dry-bulb temperature and the dew-point temperature are equal and the relative humidity is 100%.

It’s not the heat, it s the humidity aptly expresses the effect of excess moisture in the atmosphere on human comfort.

The term absolute humidity is sometimes used in describing the properties of air. Absolute humidity is similar in meaning to specific humidity, except for the units used. The term absolute humidity is used to indicate grains of water vapor per cubic foot of dry air or pounds of water vapor per cubic foot of the air-water vapor mixture, while specific humidity W indicates grains of water vapor per Pound of dry air.

Exhaustive tests over many years and involving thousands of subjects have indicated that human comfort is much more closely related to relative humidity than it is to specific humidity. Optimum values of relative humidity for most people lie between 20 and 65 percent. Below 20 percent most people find air too dry for comfort and above 65 percent, too moist.

The Measurement of Humidity - Psychrometry

The accurate measurement of partial pressures is a complex process to be performed only in a controlled atmosphere and with the scientific instruments available in a research laboratory. Humidity measurements in the field are made with more easily operated instruments, the readings from which can readily be converted into either specific humidity or relative humidity by reference to tables or charts prepared from the more accurate measurements of research laboratories.

The most convenient instrument for humidity determinations is the sling Psychrometer. The instrument consists of two standard thermometers mounted on a slender frame which can be whirled around in the air. One thermometer, the wet bulb (wb), is covered with a wick, which is saturated with water before “slinging” the instrument. The other thermometer is called the dry bulb (bd), since it has no wick. The two thermometers must be carefully matched, so that they give exactly the same reading under dry-bulb conditions.

The instrument is whirled through the air, and as evaporation occurs from the wet wick, the temperature of the wick and the reading of the wet-bulb thermometer drop. Evaporation, it will be recalled, is a cooling process. Whirling is continued until the lowest possible wet-bulb reading is obtained. At that point the difference between the readings of the two thermometers is termed the wet-bulb depression.

Let consider what the wet-bulb depression means. The lower the relative humidity of the surrounding (ambient) air, the more rapid the evaporation from the wet wick and the greater the wet-bulb depression. On the other hand if the surrounding air is moist (high RH), evaporation will be slow and the wet-bulb depression will be small. It is apparent, then, that the wet-bulb depression is a measure of relative humidity. Converting sling psychrometer readings to relative-humidity readings is done by referring to tables or charts.

Another instrument frequently used for relative humidity determinations is the wall hygrometer. It is also a wet-and-dry-bulb thermometer, but instead of being whirled it is placed either out in the wind or in the direct path of an air stream from a fan. This instrument is more commonly used by meteorologists than by air conditioning engineers.

Dry-Bulb Temperature

Dry-bulb temperature is the temperature of a substance as indicated by an ordinary thermometer. This is a simple definition, but it does not tell the whole story. Dry-bulb temperature indicates the degree of the sensible-heat content of the substance. It does not give any information whatever as to the latent-heat content. Consider two samples of air, one at 90°F and 40 percent RH, the other at 90°F and 60 percent RH. The first sample contains 0.40 x 217.3 or 87 gr of water vapor per pound of air. The second contains 0.60 X 217.3, or 130.3 gr of water vapor per pound of air. The two conditions contain far different amounts of latent heat, but the sensible-heat content of the two samples is the same, and the dry-bulb thermometer indicates that the degree of sensible heat is the same for both.

The basic heat equation for sensible-heat calculation is

H = wc(t2-t1)

Wet-Bulb Temperature

A simple definition of wet-bulb temperature is that it is the lowest temperature recorded by an ordinary thermometer whose bulb is wrapped in a wick wet with water when the thermometer is placed in a moving current of air. This definition does little, however, to explain the physical meaning of wet-bulb temperature.

Why does water evaporating from the wick lower the temperature of the wick and the thermometer? When unsaturated air is passed over a wet thermometer bulb, water evaporates from the wet surface, and the latent heat absorbed by the vaporizing water results in a lowering of the temperature of the wet surface and the thermometer bulb. As soon as the temperature of the wet surface drops below ambient or surrounding temperature, heat begins to flow from the warmer air to the cooler surface. On the other hand, as the temperature drops, the vapor pressure of the water drops which decreases evaporation and heat loss. Eventually, an equilibrium temperature is reached, and this temperature is known as the wet-bulb (wb) temperature.

The latent heat of vaporization Lv of water at the boiling point and atmospheric pressure is 970 Btu/lb. Water evaporated at other temperatures and pressures requires a different amount of heat per pound of vapour.

Heat-Content Measurements

The heat content of any given sample of air is made up of both sensible heat and latent heat. Sensible heat is reflected in the dry-bulb temperature of the air. The datum point for the sensible-heat content of dry air is 0°F in the US and 0°C in the metric system. There is also some sensible heat in the liquid before it is evaporated, and the datum point for this heat content is 32°F (0°C). Some tables and charts neglect the sensible heat of the liquid. Latent heat is the heat required to evaporate the moisture which the air contains. This evaporation occurs at the wet-bulb temperature of the air.

Total heat content of the air water vapor mixture, called enthalpy, is the sum of sensible heat in the air plus the sensible heat of the liquid plus the latent heat of the evaporated moisture plus the sensible heat to warm up the vapor from the dew-point to the dry bulb temperature. The latter quantity is called the superheat of the vapor.

Dew-Point Temperature

When an air-water-vapor mixture is cooled out of contact with liquid water, the specific humidity remains constant, but the relative humidity increases until it reaches 100%, at which point moisture begins to condense. The temperature at this point is termed the dew-point temperature (dp). To find the dew-point temperature at any specific humidity condition, it is merely necessary to determine the saturation temperature of air at the same specific humidity.

Since air is saturated at the dew point, dew-point temperature is indicative of the moisture content of the air and is therefore also a measure of the latent-heat content of the air-water vapor mixture.

Relationships among Dry-Bulb and Wet-Bulb Temperatures, Dew Point, Relative Humidity, and Enthalpy

If air is saturated with moisture at any temperature (100% RH there will be no wet-bulb depression. Also, at saturation, any lowering of the temperature would result in condensation. Consequently, at saturation, wet bulb = dry bulb = dew Point.

In any unsaturated mixture of air and water vapor the relation among dp, db, and wb is somewhat more complex. The relationship can be clarified by reference to the diagram below.

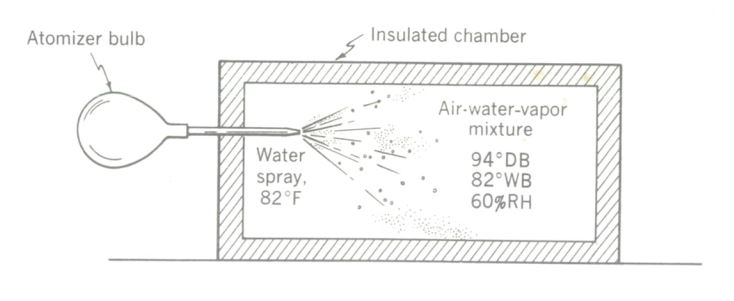
An adiabatic (constant-heat) process taking place in a sealed chamber, showing how WB, DB, and DP are related.

Suppose a perfectly insulated container is filled with an unsaturated air-water-vapor mixture at, say, 94°F DB and 60 percent RH. Pressure is assumed to remain constant, and the insulation will prevent any heat gains or losses.

Now let us inject a fine spray of water at the wet bulb temperature of 82°F into the chamber. Since perfect insulation was assumed, no further heat will enter or depart from the chamber, and any thermodynamic processes which take place will occur at constant heat. It will be recalled that such constant-heat processes are called adiabatics.

The water spray will evaporate until a saturated condition is reached within the chamber. The heat required to evaporate the water must be drawn from the sensible heat of the air, since it cannot come from outside the container. The sensible heat transferred from the air equals the increase in latent heat in the evaporated moisture. Total heat remains constant. As sensible heat is withdrawn from the air, its dry-bulb temperature falls. As moisture is added to the air, dew-point temperature rises. As saturation is reached, the db will have fallen to 82°F, the DP will have risen to 82°F, and DB = WB = DP. The total heat (enthalpy) has remained constant, at 45.98 Btu per lb.

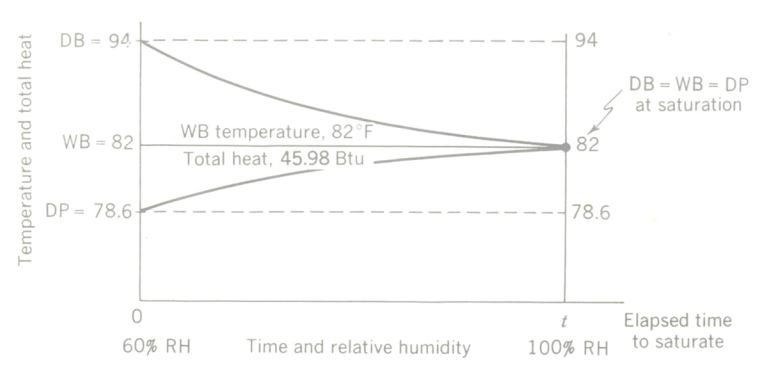
Temperature-total heat-time diagram of an adiabatic psychrometric process. At saturation, dry-bulb temperature = wet-bulb temperature = dew point. Total heat content (enthalpy) remains unchanged, since the sealed, insulated chamber allows no heat energy to be gained or lost.

The wet-bulb temperature is the same at saturation as it was at the initial condition.

Note that, although air can be cooled (that is, its db temperature will drop) by evaporating water into the air, the wb temperature remains unchanged, and relative humidity (RH) increases.

The process just described can be illustrated by a temperature-total heat-time diagram above. Such a plot shows clearly that the wet-bulb temperature and the total heat both stay constant during adiabatic saturation. In the actual practice of air conditioning, psychometric processes do not occur under the ideal, controlled conditions of the illustration presented here, but many humidification and dehumidification processes approach the adiabatic situation closely enough that the errors introduced by assuming adiabatic conditions can be neglected.

The foregoing discussions should serve to establish the following:

Dry-bulb temperature is associated only with the sensible heat of the air in air-water vapor mixtures.
Dew-point temperature is an indication of the specific humidity and therefore of the latent-heat content of air-water vapor mixtures.
Wet-bulb temperature is constant as long as total heat remains constant. It is the temperature approached by both the DB and the DP as saturation is imminent. At saturation, db = wb = dp
Enthalpy is the total heat content of the air-water vapor mixture. It is made up of the sensible heat of the air (from 0°F to the DB temperature) plus the sensible heat of the liquid (from 32°F to the wb temperature) plus the latent heat of the evaporated moisture (Lv being taken at the wb temperature) plus heat to superheat the vapor (from the wb temperature at which evaporation occurred to the mixture db temperature).